1. VALOR PRESENTE LÍQUIDO (VPL)

O Valor Presente Líquido (VPL) é utilizado para calcular atratividade de investimentos. Supondo que você faça um investimento inicial de R$100 mil reais em um projeto e espera fluxo de caixa de R$10mil mensais, dada a taxa de atratividade (juros), você deseja saber se o projeto é viável ou não.

Embora o cálculo seja bem direto, precisamos observar uma coisa importante. Como os fluxos são mensais, a cada mês os R$10 mil vão perdendo valor. Contudo, os R$100 mil investidos inicialmente foram investidos com valores correntes.

Desta forma, precisamos descontar cada fluxo de caixa que ocorrerá para saber o quanto ele vale, hoje, e comparar este resultado com o valor investido.

Na planilha usamos a fórmula: VPL(TAXA,valor1,valor2; ...)

Onde taxa é a taxa de desconto sobre o intervalo de um período.

Valor1; valor2;...são argumentos de 1 a 29 que representam os pagamentos e a receita.

• Valor1; valor2;... devem ter o mesmo intervalo de tempo entre eles e ocorrer ao final de cada período.
• VPL utiliza a ordem de valor1; valor2;... para interpretar a ordem de fluxos de caixa. Certifique-se de fornecer os valores de pagamentos e receita na seqüência correta.
• Argumentos que são números, células vazias, valores lógicos ou representações em forma de texto de números são contados; os argumentos que são valores de erro ou texto que não podem ser traduzidos em números são ignorados.
• Se um argumento for uma matriz ou referência, apenas os números da matriz ou referência serão contados. Células vazias, valores lógicos, valores de texto ou de erro na matriz ou referência são ignorados.

Comentários

• O investimento de VPL começa um período antes da data do fluxo de caixa de valor 1 e termina com o último fluxo de caixa na lista. O cálculo de VPL baseia-se em fluxos e caixa futuros. Se o seu primeiro fluxo de caixa ocorrer no início do primeiro período, o primeiro valor deverá ser incluído ao resultado VPL, e não nos valores de argumentos. Para obter mais informações, veja os exemplos abaixo.
• Se n for o número de fluxos de caixa na lista de valores, a fórmula para VPL será:

• VPL assemelha-se à função VP (valor presente). A principal diferença entre VP e VPL é que a primeira permite que os fluxos de caixa comecem no final ou no início do período. Diferentemente dos valores de fluxo de caixa da variável VPL, os fluxos de caixa VP devem ser constantes durante o período de investimento. Para obter informações sobre anuidades e funções financeiras, consulte VP.
• VPL também está relacionado à função TIR (taxa interna de retorno). TIR é a taxa para qual VPL é igual a zero: VPL(TIR(...); ...)=0

Exemplo:

Supondo o fluxo de caixa abaixo com taxa de desconto 5% ao mês, queremos saber se o VPL é positivo ou não.

Se o fluxo for positivo, então o projeto é viável. Se for negativo a taxa é menor que a esperada e é melhor deixá-lo de lado.

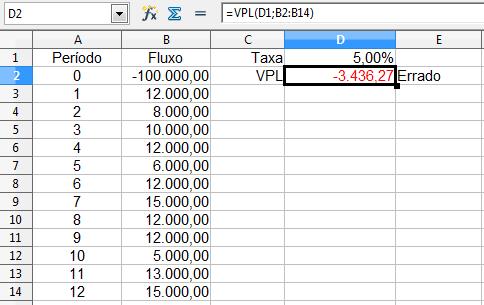
Infelizmente, a função VPL pode apresentar um pequeno problema para os mais incautos. O VPL é definido como o valor presente dos fluxos de caixa menos o valor inicial do investimento, isto é:

VPL = VP (Fluxos) - Investimento

Se calcularmos o VP utilizando uma tabela e subtrairmos do resultado o valor do investimento obtemos: R$ -3.608,09

Este resultado é bem diferente do resultado encontrado pela função VPL. Então, qual resultado está correto? Observe que no primeiro exemplo incluímos o valor do investimento no cálculo do VPL. Quando fazemos isso o valor do investimento é descontado e cada valor subseqüente é descontado no período seguinte. Em outras palavras, todos os valores são descontados nos períodos errados.

Existem várias formas de se corrigir este problemas. Uma delas é usar o exemplo anterior com a função VP e subtração do valor investido.

Outra opção é notar que o valor original de um valor descontado nada mais é do que o valor descontado multiplicado pelo coeficiente de desconto, isto é:

à VP*(1+i) = VF

Se o coeficiente é (1+i), então tudo que precisamos fazer é multiplicar o resultado por este coeficiente:

=VPL (Taxa;Investimento:Fluxos)*(1+i)

Outra maneira e calcular o VPL dos fluxos e depois descontar o valor do investimento

=VPL(TAXA,Valor1:Valorn)-VP

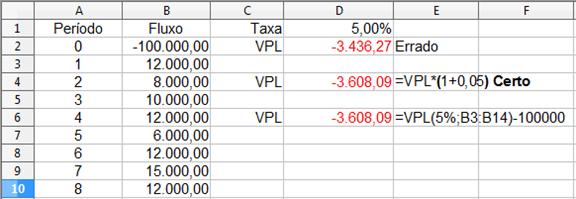
A figura a seguir mostra as diferentes opções de cálculo:

2. TAXA INTERNA DE RETORNO (TIR)

A Taxa Interna de Retorno (TIR) é outra medida de investimento, porém, diferentemente do VPL, a TIR não retorna um valor monetário. Ela retorna um percentual.

Na planilha; TIR (valores;estimativa)

Valores é uma matriz ou uma referência a células que contêm números cuja taxa interna de retorno se deseja calcular.

• Valores deve conter pelo menos um valor positivo e um negativo para calcular a taxa interna de retorno.
• TIR usa a ordem de valores para interpretar a ordem de fluxos de caixa. Certifique-se de inserir os valores de pagamentos e rendas na seqüência desejada.
• Se uma matriz ou argumento de referência contiver texto, valores lógicos ou células em branco, estes valores serão ignorados.

Estimativa é um número que se estima ser próximo do resultado de TIR.

• A planilha usa uma técnica iterativa para calcular TIR. Começando por estimativa, TIR refaz o cálculo até o resultado ter uma precisão de 0,00001 por cento. Se TIR não puder localizar um resultado que funcione depois de 20 tentativas, o valor de erro #NÚM! será retornado.
• Na maioria dos casos, não é necessário fornecer estimativa para o cálculo de TIR. Se estimativa for omitida, será considerada 0,1 (10 por cento).
• Se TIR fornecer o valor de erro #NÚM!, ou se o resultado não for próximo do esperado, tente novamente com um valor diferente para estimativa.

O percentual retornado pela TIR é a taxa de juros que zero o VPL. Para compreender melhor o que isso significa, vamos retornar ao exemplo. Observe a figura:

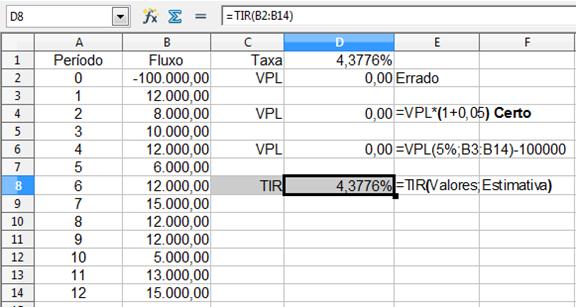
A TIR é calculada em cima do investimento e fluxos de caixa. O resultado final é aproximadamente 4,3776%. Em seguida, utilizamos este valor para calcular o VPL. Como foi observado, a TIR é a taxa que zera o VPL. Em outras palavras, a TIR representa a taxa máxima que o projeto agüenta antes de se tornar negativo.