Sistemas de Amortização

Quando se contrai um empréstimo ou se recorre a um financiamento, evidentemente, o valor recebido nesta operação, ou seja, o principal terá que ser restituído à financeira, acrescido dos juros.

As formas de devolução do principal, mais juros são denominadas de Sistemas de Amortização. Os Sistemas de Amortização mais utilizados são:r

Sistema Francês de Amortização – PRICE

Este sistema também é conhecido como Sistema Price e é muito utilizado em todos os setores financeiros, principalmente nas compras a prazo de bens de consumo, através do crédito direto ao consumidor.

No Sistema Price, as prestações são iguais e sucessivas, onde cada prestação é composta por duas parcelas: juros e amortização do capital; cujo cálculo baseia-se numa série uniforme de pagamentos.

Situação problema

Calcular os valores das parcelas de juros e amortizações referentes a um empréstimo de R$ 1.000, pelo sistema PRICE, a uma taxa de 4 % a.m. e prazo de 10 meses.

Para calcular a prestação usamos a expressão , assim:

R = 1.000 .[0,04.(1+ 0,04)¹⁰ ] / [(1+ 0,04)¹⁰ -1] = 123,29

Os juros são calculados sempre sobre o saldo devedor:

J₁ = 1.000 x 0,04 = 40 (e assim por diante

Amortização igual à prestação subtraído-se os juros: A = R – J.

n	Prestação	Juro	Amortização	Saldo Devedor
0	-	-	-	1.000,00
1	123,29	40,00	83,29	916,71
2	123,29	36,67	86,62	830,09
3	123,29	33,20	90,09	740,00
4	123,29	29,60	93,69	646,31
5	123,29	25,85	97,44	548,87
6	123,29	21,95	101,34	447,53
7	123,29	17,90	105,39	342,14
8	123,29	13,69	109,61	232,54
9	123,29	9,30	113,99	118,55
10	123,29	4,74	118,55	0,00

Sistema de Amortização Constante – SAC

Este sistema é muito utilizado em financiamentos internacionais de bancos de desenvolvimento e no sistema financeiro de habitação brasileiro, bem como em financiamentos de longos prazos.

As prestações do Sistema SAC são sucessivas e decrescentes em progressão aritmética, cujo valor de cada prestação é composto por uma parcela de juros e outra de amortização constante do capital.

Situação problema

Calcular os valores das parcelas de juros e amortizações referentes a um empréstimo de R$ 1.000, pelo sistema SAC, a uma taxa de 4 % a.m. e prazo de 10 meses.

Para calcular a amortização divide-se o valor financiado pelo numero de parcelas, assim no exemplo temos: A = 1.000 / 10 = 100

Os juros são calculados sobre o saldo devedor:

J₁ = 10.000 _x 0,04 = 400 (e assim por diante)

Prestação igual à soma da amortização e juros: R = A + J.

n	Prestação	Juro	Amortização	Saldo Devedor
0	-	-	-	1.000,00
1	140,00	40,00	100,00	900,00
2	136,00	36,00	100,00	800,00
3	132,00	32,00	100,00	700,00
4	128,00	28,00	100,00	600,00
5	124,00	24,00	100,00	500,00
6	120,00	20,00	100,00	400,00
7	116,00	16,00	100,00	300,00
8	112,00	12,00	100,00	200,00
9	108,00	8,00	100,00	100,00
10	104,00	4,00	100,00	0,00

Sistema de Amortização Misto (SAM)

Por este sistema, o devedor paga o empréstimo em prestações, tais que cada uma delas é a média aritmética entre os valores encontrados para as prestações do sistema PRICE e do SAC. E claro que isso implica que os juros, amortizações e saldos devedores no SAM, em cada período, também constituam cada um, a média aritmética entre juros, amortizações e saldos devedores dos sistemas PRICE e SAC. Mas na prática nem sempre é conveniente calcular esses valores dessa forma e apenas as prestações são calculadas como médias aritméticas.

Chamando de R a prestação do sistema PRICE e de P₁, P₂, ..., P_n as prestações do SAC, para calcular as prestações P’₁, P’₂ P’_n do SAM, basta fazer:

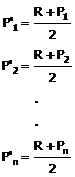
Calculadas as prestações, o demonstrativo deve ser elaborado, como no sistema PRICE, linha por linha.

Sistema Americano de Amortização

Por este sistema, o devedor paga os juros periodicamente; o valor emprestado é pago no final do prazo estipulado para o empréstimo.

Chamando de PV o valor emprestado com a taxa de juros i, os juros pagos em cada período são iguais e calculados como:

J = PV . i

Terminado o prazo, o devedor, no último pagamento, além dos juros, salda o capital emprestado PV.

Observe-se que, por esse sistema, é indiferente que o regime de juros seja simples ou composto, pois, como os juros são pagos periodicamente, o saldo devedor é sempre o mesmo, o que não muda o valor básico para o cálculo dos juros.

Sistema de Pagamento Único

Este é o sistema mais simples e é muito utilizado para financiamentos industriais de capital de giro. O tomador simplesmente paga os juros e amortiza o principal no final do empréstimo.

Os juros cobrados poderão ser simples ou compostos, de acordo com o contrato estipulado.

Sistema de Juros Antecipados

Por este sistema, o devedor paga o total dos juros na data da liberação do empréstimo. Como no sistema anterior, os juros poderão ser simples ou compostos.

É claro que, se os juros são pagos antecipadamente, o valor liberado como empréstimo (empréstimo efetivo) não coincide com o solicitado pelo devedor, o que faz com que a taxa efetiva a que ele se obriga seja diferente da taxa nominal contratada. Com os juros pagos antecipadamente, apenas será paga no final a quantia solicitada como empréstimo.

Chamando de PV o valor efetivamente liberado (empréstimo efetivo) e de FV o pagamento final (empréstimo contratado) e supondo que o empréstimo seja feito à taxa i de juros simples e pelo prazo de n períodos, o valor liberado será:

PV = FV – FV . i . n

ou:

PV = FV.(1 – i.n)

O que corresponde ao valor solicitado deduzido com desconto comercial simples.

Para calcular a taxa efetiva i_e paga pelo devedor, basta usar a equação do montante de juros simples considerando o empréstimo efetivo como VP e o empréstimo contratado como VF. Tem-se, então:

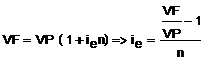
Se o empréstimo foi contratado com juros compostos, o valor liberado será:

PV = FV - (FV (1 + i)ⁿ - FV)

Juro em uma capitalização composta

ou:

PV = FV - FV(1 + i)ⁿ + FV

ou, ainda: PV = FV(2 - (1 + i)ⁿ)

e a taxa efetiva será:

A taxa efetiva é obtida isolando-se a taxa na equação do juro composto VF = VP(1+i)ⁿ

Situação problema

Considere-se um empréstimo de R$ 1.000,00, à taxa de 4% a.m. pelo prazo de dez meses. Se os juros são cobrados antecipadamente, calcular o valor liberado, o valor a ser pago no final do prazo e a taxa efetiva:

a) para o regime de juros simples;

b) para o regime de juros compostos.

Solução:

a) PV = FV (1 - in) = 1.000 (1 - 0,04 _x 10) = 600

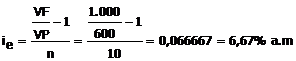
Outra solução:

J = VP.i.n = 1.000 . 0,04 . 10 = 400 (juros antecipados)

1.000 - 400 = 600 (valor liberado)

VF = VP (1 + i_e n) => 1.000 = 600(1+i_e.10) => i_e = 0,0666667= 6,66% a.m.

No caso de juro composto

b) PV = FV(2 - (1+i)ⁿ ) = 1.000(2 - (1+0,04)¹⁰) = 519,76

Taxa efetiva:

Outra solução:

VF = VP (1 + i)ⁿ = 1.000 (1 + 0,04)¹⁰ = 1.480,24

Juros = VF – VP = 1.480,24 - 1000 = 480,24 (juros antecipados)

Valor liberado => VP – J =1.000 – 480,24 = 519,76

Resposta:

a) No regime de juros simples, o valor liberado é R$ 600,00, o valor a ser pago no final é R$ 1.000,00 e a taxa efetiva que o devedor paga é 6,67% a.m.;

b) No regime de juros compostos, o valor liberado é R$ 519,76, o valor a ser pago no final é R$ 1.000,00 e a taxa efetiva que o devedor paga é 6,76% a.m.